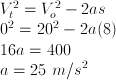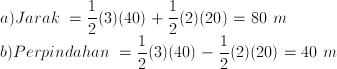Fisikastudycenter.com- Contoh Soal dan Pembahasan tentang
Gerak Lurus Berubah Beraturan (GLBB) dan Gerak Lurus Beraturan (GLB),
termasuk gerak vertikal ke atas dan gerak jatuh bebas, materi fisika
kelas 10 (X) SMA. Mencakup penggunaan rumus-rumus GLBB/GLB dan membaca
grafik V-t.
Soal No. 1 Batu bermassa 200 gram dilempar lurus ke atas dengan kecepatan awal 50 m/s.

Jika percepatan gravitasi ditempat tersebut adalah 10 m/s
2, dan gesekan udara diabaikan, tentukan :
a) Tinggi maksimum yang bisa dicapai batu
b) Waktu yang diperlukan batu untuk mencapai ketinggian maksimum
c) Lama batu berada diudara sebelum kemudian jatuh ke tanah
Pembahasan
a) Saat batu berada di titik tertinggi, kecepatan batu adalah nol dan
percepatan yang digunakan adalah percepatan gravitasi. Dengan rumus
GLBB:

b) Waktu yang diperlukan batu untuk mencapai titik tertinggi:

c) Lama batu berada di udara adalah dua kali lama waktu yang diperlukan untuk mencapai titik tertinggi.
t = (2)(5) = 10 sekon
Soal No. 2Sebuah
mobil bergerak dengan kelajuan awal 72 km/jam kemudian direm hingga
berhenti pada jarak 8 meter dari tempat mulainya pengereman. Tentukan
nilai perlambatan yang diberikan pada mobil tersebut!
Pembahasan Ubah dulu satuan km/jam menjadi m/s kemudian gunakan persamaan untuk GLBB diperlambat:
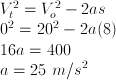
Soal No. 3 Perhatikan grafik berikut ini.

Dari grafik diatas tentukanlah:
a. jarak tempuh gerak benda dari t = 5 s hingga t = 10 s
b. perpindahan benda dari t = 5 s hingga t = 10 s
Pembahasan
Jika diberikan graik V (kecepatan) terhadap t (waktu) maka untuk
mencari jarak tempuh atau perpindahan cukup dari luas kurva grafik V-t.
Dengan catatan untuk jarak, semua luas bernilai positif, sedang untuk
menghitung perpindahan, luas diatas sumbu t bernilai positif, di bawah
bernilai negatif.
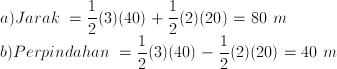 Soal No. 4
Soal No. 4 Seekor semut bergerak dari titik A menuju titik B pada seperti terlihat pada gambar berikut.
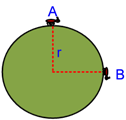
Jika r = 2 m, dan lama perjalanan semut adalah 10 sekon tentukan:
a) Kecepatan rata-rata gerak semut
b) Kelajuan rata-rata gerak semut
Pembahasan Terlebih dahulu tentukan nilai perpindahan dan jarak si semut :
Jarak yang ditempuh semut adalah dari A melalui permukaan lengkung
hingga titik B, tidak lain adalah seperempat keliling lingkaran.
Jarak =
1/
4 (2πr) =
1/
4 (2π x 2) = π meter
Perpindahan semut dilihat dari posisi awal dan akhirnya , sehingga
perpindahan adalah dari A tarik garis lurus ke B. Cari dengan
phytagoras.
Perpindahan = √ ( 2
2 + 2
2 ) = 2√2 meter.
a) Kecepatan rata-rata = perpindahan : selang waktu
Kecepatan rata-rata = 2√2 meter : 10 sekon = 0,2√2 m/s
b) Kelajuan rata-rata = jarak tempuh : selang waktu
Kelajuan rata- rata = π meter : 10 sekon = 0,1 π m/s
Soal No. 5
Pesawat Burung Dara Airlines berangkat dari kota P menuju arah timur
selama 30 menit dengan kecepatan konstan 200 km/jam. Dari kota Q
berlanjut ke kota R yang terletak 53
o terhadap arah timur ditempuh selama 1 jam dengan kecepatan konstan 100 km/jam.

Tentukan:
a) Kecepatan rata-rata gerak pesawat
b) Kelajuan rata-rata gerak pesawat
Pembahasan Salah satu cara :
Terlebih dahulu cari panjang PQ, QR, QR', RR', PR' dan PR

PQ = V
PQ x t
PQ = (200 km/jam) x (0,5) jam = 100 km
QR = V
QR x t
QR = (100 km/jam) x (1 jam) = 100 km
QR' = QR cos 53
o = (100 km) x (0,6) = 60 km
RR' = QR sin 53
o = (100 km) x (0,8) = 80 km
PR' = PQ + QR' = 100 + 60 = 160 km
PR = √[ (PR' )
2 + (RR')
2 ]
PR = √[ (160 )
2 + (80)
2 ] = √(32000) = 80√5 km
Jarak tempuh pesawat = PQ + QR = 100 + 100 = 200 km
Perpindahan pesawat = PR = 80√5 km
Selang waktu = 1 jam + 0,5 jam = 1,5 jam
a) Kecepatan rata-rata = perpindahan : selang waktu = 80√5 km : 1,5 jam = 53,3 √5 km/jam
b) Kelajuan rata-rata = jarak : selang waktu = 200 km : 1,5 jam = 133,3 km/jam
Soal No. 6 Diberikan grafik kecepatan terhadap waktu seperti gambar berikut:

Tentukan besar percepatan dan jenis gerak dari:
a) A - B
b) B - C
c) C - D
Pembahasan Mencari percepatan (a) jika diberikan grafik V-t :
a = tan θ
dengan θ adalah sudut kemiringan garis grafik terhadap horizontal dan
tan suatu sudut adalah sisi depan sudut dibagi sisi samping sudut. Ingat
: tan-de-sa
a) A - B
a = (2 − 0) : (3− 0) =
2/
3 m/s
2(benda bergerak lurus berubah beraturan / GLBB dipercepat)
b) B - C
a = 0 (garis lurus, benda bergerak lurus beraturan / GLB)
c) C - D
a = (5 − 2) : (9 − 7) =
3/
2 m/s
2 (benda bergerak lurus berubah beraturan / GLBB dipercepat)
Soal No. 7 Dari gambar berikut :

Tentukan:
a) Jarak tempuh dari A - B
b) Jarak tempuh dari B - C
c) Jarak tempuh dari C - D
d) Jarak tempuh dari A - D
Pembahasan a) Jarak tempuh dari A - B
Cara Pertama
Data :
V
o = 0 m/s
a = (2 − 0) : (3− 0) =
2/
3 m/s
2 t = 3 sekon
S = V
o t +
1/
2 at
2 S = 0 +
1/
2 (
2/
3 )(3)
2 = 3 meter
Cara Kedua
Dengan mencari luas yang terbentuk antara titik A, B dang angka 3 (Luas
Segitiga = setengah alas x tinggi) akan didapatkan hasil yang sama
yaitu 3 meter
b) Jarak tempuh dari B - C
Cara pertama dengan Rumus GLB
S = Vt
S = (2)(4) = 8 meter
Cara kedua dengan mencari luas yang terbentuk antara garis B-C, angka 7 dan angka 3 (luas persegi panjang)
c) Jarak tempuh dari C - D
Cara Pertama
Data :
V
o = 2 m/s
a =
3/
2 m/s
2 t = 9 − 7 = 2 sekon
S = V
o t +
1/
2 at
2 S = (2)(2) +
1/
2 (
3/
2 )(2)
2 = 4 + 3 = 7 meter
Cara kedua dengan mencari luas yang terbentuk antara garis C-D, angka 9 dan angka 7 (luas trapesium)
S = 1/2 (jumlah sisi sejajar) x tinggi
S = 1/2 (2+5)(9-7) = 7 meter.
d) Jarak tempuh dari A - D
Jarak tempuh A-D adalah jumlah dari jarak A-B, B-C dan C-D
Soal No. 8 Mobil A dan B dalam kondisi diam terpisah sejauh 1200 m.

Kedua mobil kemudian bergerak bersamaan saling mendekati dengan kecepatan konstan masing-masing V
A = 40 m/s dan V
B = 60 m/s.
Tentukan:
a) Jarak mobil A dari tempat berangkat saat berpapasan dengan mobil B
b) Waktu yang diperlukan kedua mobil saling berpapasan
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
Pembahasan
Waktu tempuh mobil A sama dengan waktu tempuh mobil B, karena
berangkatnya bersamaan. Jarak dari A saat bertemu misalkan X, sehingga
jarak dari B (1200 − X)
t
A = t
B SA/
VA =
SB/
VB ( x )/
40 =
( 1200 − x ) /
60 6x = 4( 1200 − x )
6x = 4800 − 4x
10x = 4800
x = 480 meter
b) Waktu yang diperlukan kedua mobil saling berpapasan
x = V
A t
480 = 40t
t = 12 sekon
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
S
B =V
B t = (60) (12) = 720 m
Soal No. 9 Diberikan grafik kecepatan terhadap waktu dari gerak dua buah mobil, A dan B.

Tentukan pada jarak berapakah mobil A dan B bertemu lagi di jalan jika keduanya berangkat dari tempat yang sama!
Pembahasan Analisa grafik:
Jenis gerak A → GLB dengan kecepatan konstan 80 m/s
Jenis gerak B → GLBB dengan percepatan a = tan α = 80 : 20 = 4 m/s
2 Kedua mobil bertemu berarti jarak tempuh keduanya sama, misal keduanya bertemu saat waktu t
S
A = S
B V
A t =V
oB t +
1/
2 at
2 80t = (0)t +
1/
2 (4)t
2 2t
2 − 80t = 0
t
2 − 40t = 0
t(t − 40) = 0
t = 0 sekon atau t = 40 sekon
Kedua mobil bertemu lagi saat t = 40 sekon pada jarak :
S
A = V
A t = (80)(40) = 3200 meter
Soal No. 10 (Gerak Vertikal ke Bawah / Jatuh Bebas) Sebuah benda jatuh dari ketinggian 100 m. Jika percepatan gravitasi bumi 10 m/s
2 tentukan:
a) kecepatan benda saat t = 2 sekon
b) jarak tempuh benda selama 2 sekon
c) ketinggian benda saat t = 2 sekon
d) kecepatan benda saat tiba di tanah
e) waktu yang diperlukan benda hingga tiba di tanah
Pembahasan a) kecepatan benda saat t = 2 sekon
Data :
t = 2 s
a = g = 10 m/s
2 V
o = 0 m/s
V
t = .....!
V
t = V
o + at
V
t = 0 + (10)(2) = 20 m/s
c) jarak tempuh benda selama 2 sekon
S = V
ot +
1/
2at
2 S = (0)(t) +
1/
2 (10)(2)
2 S = 20 meter
c) ketinggian benda saat t = 2 sekon
ketinggian benda saat t = 2 sekon adalah tinggi mula-mula dikurangi jarak yang telah ditempuh benda.
S = 100 − 20 = 80 meter
d) kecepatan benda saat tiba di tanah
V
t2 = V
o2 + 2aS
V
t2 = (0) + 2 aS
V
t = √(2aS) = √[(2)(10)(100)] = 20√5 m/s
e) waktu yang diperlukan benda hingga tiba di tanah
V
t = V
0 + at
20√5 = (0) + (10) t
t = 2√5 sekon
Soal No. 11
Besar kecepatan suatu partikel yang mengalami perlambatan konstan
ternyata berubah dari 30 m/s menjadi 15 m/s setelah menempuh jarak
sejauh 75 m. Partikel tersebut akan berhenti setelah menempuh jarak....
A. 15 m
B. 20 m
C. 25 m
D. 30 m
E. 50 m
(Soal SPMB 2003)
PembahasanData pertama:
Vo = 30 m/s
Vt = 15 m/s
S = 75 m
Dari ini kita cari perlambatan partikel sebagai berikut:
Vt
2 = Vo
2 − 2aS
15
2 = 30
2 − 2a(75)
225 = 900 − 150 a
150 a = 900 − 225
a = 675 /150 = 4, 5 m/s
2 Besar perlambatannya adalah 4,5 m/s
2
(Kenapa tidak negatif? Karena dari awal perhitungan tanda negatifnya
sudah dimasukkan ke dalam rumus, jika ingin hasil a nya negatif, gunakan
persamaan Vt
2 = Vo
2 + 2aS)
Data berikutnya:
Vo = 15 m/s
Vt = 0 m/s (hingga berhenti)
Jarak yang masih ditempuh:
Vt
2 = Vo
2 − 2aS
0
2 = 15
2 − 2(4,5)S
0 = 225 − 9S
9S = 225
S = 225/9 = 25 m
Soal No. 12 Sebuah benda dijatuhkan dari ujung sebuah menara tanpa kecepatan awal. Setelah 2 detik benda sampai di tanah (g = 10 m s
2). Tinggi menara tersebut …
A. 40 m
B. 25 m
C. 20 m
D. 15 m
E. 10 m
(EBTANAS 1991)
Pembahasan Data:
ν
o = 0 m/s (jatuh bebas)
t = 2 s
g = 10 m s
2 S = .....!
S = ν
o t + 1/2 gt
2 S = (0)(2) + 1/2 (10)(2)
2S = 5(4) = 20 meter
Soal No. 13 Sebuah benda dijatuhkan dari ketinggian h di atas tanah. Setelah sampai di tanah kecepatannya 10 m s
–1, maka waktu yang diperlukan untuk mencapai ketinggian
1/
2 h dari tanah (g = 10 m. s
−2 ) adalah.....
A. 1/2 √2 sekon
B. 1 sekon
C. √2 sekon
D. 5 sekon
E. 5√2 sekon
(Soal Ebtanas 2002)
Pembahasan Data:
Untuk jarak tempuh sejauh S
1 = h
ν
o = 0 ms
–1 ν
t = 10 m s
–1
ν
t = ν
o + at
10 = 0 + 10t
t = 1 sekon -> t
1
Untuk jarak tempuh sejauh S
2 =
1/
2 h
t
2 =......
Perbandingan waktu tempuh:
 Soal No. 14
Soal No. 14 Sebuah batu dijatuhkan dari puncak menara yang tingginya 40 m di atas tanah. Jika g = 10 m s
–2, maka kecepatan batu saat menyentuh tanah adalah.…
A. 20√2 m s
–1 B. 20 m s
–1 C. 10√2 m s
–1 D. 10 m s
–1 E. 4√2 m s
–1(Ebtanas Fisika 1996)
Pembahasan Jatuh bebas, kecepatan awal nol, percepatan a = g = 10 m s
–2  Soal No. 15
Soal No. 15 Mobil massa 800 kg bergerak lurus dengan kecepatan awal 36 km.jam
–1 setelah menempuh jarak 150 m kecepatan menjadi 72 km. jam
–1. Waktu tempuh mobil adalah...
A. 5 sekon
B. 10 sekon
C. 17 sekon
D. 25 sekon
E. 35 sekon
(Ujian Nasional 2009)
Pembahasan Data soal:
m = 800 kg
ν
o = 36 km/jam = 10 m/s
ν
t = 72 km/jam = 20 m/s
S = 150 m
t = ..........
Tentukan dulu percepatan gerak mobil (a) sebagai berikut:
ν
t2 = ν
o2 + 2aS
20
2 = 10
2 + 2a(150)
400 = 100 + 300 a
400 − 100 = 300 a
300 = 300 a
a =
300/
300 = 1 m/s
2 Rumus kecepatan saat t:
ν
t = ν
o + at
20 = 10 + (1)t
t = 20 − 10 = 10 sekon
Catatan:
Massa mobil (m) tidak diperlukan dalam perhitungan.